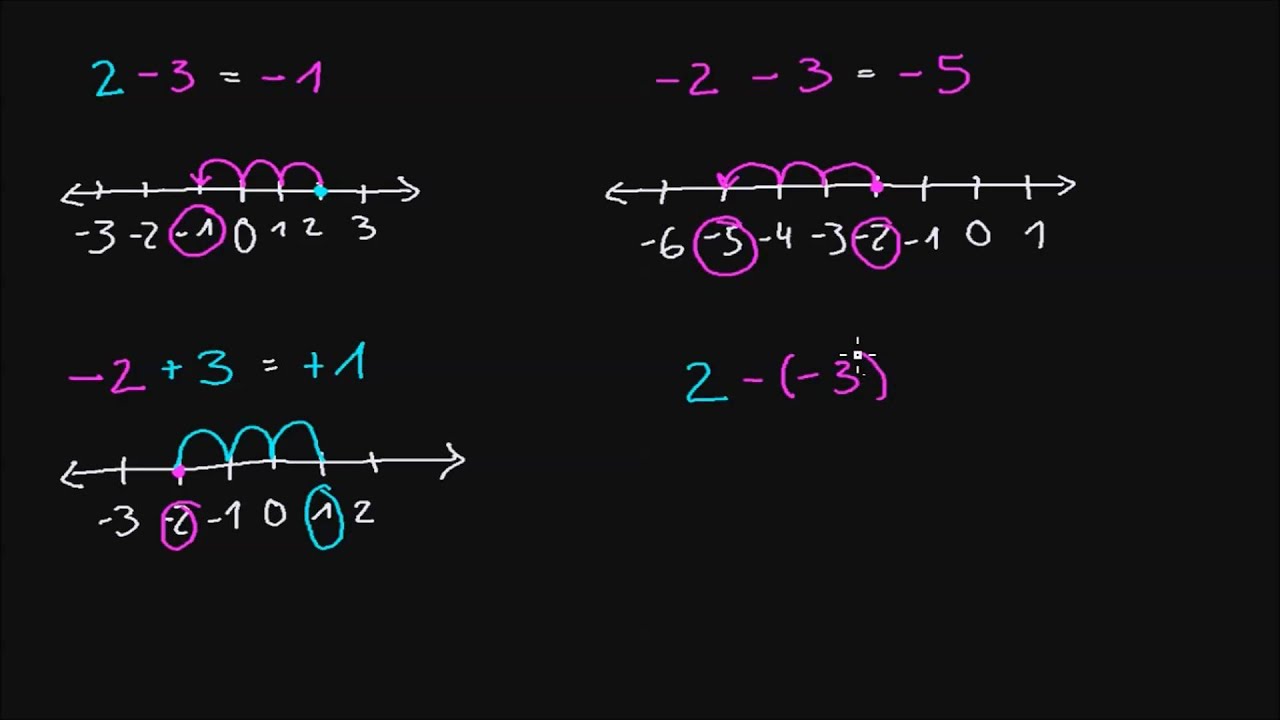Stell dir vor, du stehst auf einem Berg und wanderst 5 Meter bergab. Wie beschreibst du diese Veränderung in der Höhe? Mit negativen Zahlen! Sie eröffnen uns eine Welt jenseits der Null und ermöglichen es, Veränderungen in beide Richtungen zu quantifizieren. Dieser Artikel taucht ein in die Welt des Rechnens mit negativen Zahlen, speziell Addition und Subtraktion. Du wirst lernen, wie man mit diesen Zahlen umgeht, und ihre Bedeutung in verschiedenen Bereichen entdecken.
Negative Zahlen sind essenziell für unser Verständnis von Mathematik und Naturwissenschaften. Sie repräsentieren Werte unterhalb des Nullpunkts und ermöglichen es uns, Konzepte wie Schulden, Temperaturen unter dem Gefrierpunkt oder Höhenunterschiede präzise darzustellen. Von der Finanzwelt bis zur Physik spielen negative Zahlen eine entscheidende Rolle. Doch wie rechnet man mit ihnen?
Das Rechnen mit negativen Zahlen mag zunächst verwirrend erscheinen, doch mit ein paar einfachen Regeln wird es schnell verständlich. Die Addition und Subtraktion negativer Zahlen folgt einer klaren Logik, die sich mit etwas Übung leicht verinnerlichen lässt. In diesem Artikel werden wir diese Regeln Schritt für Schritt erklären und mit anschaulichen Beispielen veranschaulichen.
Die Geschichte der negativen Zahlen reicht weit zurück. Schon im antiken China wurden sie verwendet, um Schulden zu repräsentieren. Im Laufe der Jahrhunderte wurden sie von Mathematikern weiterentwickelt und in das Zahlensystem integriert. Heute sind negative Zahlen ein unverzichtbarer Bestandteil der Mathematik und ihrer Anwendungen.
Von der Wettervorhersage bis zur Buchhaltung – negative Zahlen begegnen uns im Alltag ständig. Sie helfen uns, die Welt um uns herum zu verstehen und zu beschreiben. Das Verständnis des Rechnens mit negativen Zahlen ist daher eine wichtige Grundlage für viele Bereiche des Lebens.
Die Addition negativer Zahlen lässt sich mit der Vorstellung von Bewegungen auf einem Zahlenstrahl veranschaulichen. (-5) + (-3) bedeutet, von -5 aus drei Schritte weiter nach links zu gehen, was -8 ergibt. Die Subtraktion negativer Zahlen kann als Addition des positiven Gegenstücks interpretiert werden. (-5) - (-3) ist dasselbe wie (-5) + 3, was -2 ergibt.
Vorteile des Rechnens mit negativen Zahlen:
1. Präzise Darstellung von Veränderungen: Negative Zahlen ermöglichen die exakte Beschreibung von Verlusten, Abnahmen oder Rückgängen.
2. Erweiterung des Zahlensystems: Sie ergänzen die positiven Zahlen und vervollständigen unser Verständnis von Zahlen.
3. Anwendungsvielfalt: Von der Physik bis zur Finanzwelt finden negative Zahlen in zahlreichen Bereichen Anwendung.
Tipps und Tricks: Stellen Sie sich einen Zahlenstrahl vor, um die Operationen zu visualisieren. Merke: Minus mal Minus ergibt Plus.
Häufig gestellte Fragen:
1. Was ist eine negative Zahl? Eine Zahl kleiner als Null.
2. Wie addiert man negative Zahlen? Ähnlich wie positive Zahlen, nur in die negative Richtung.
3. Wie subtrahiert man negative Zahlen? Addiere den positiven Gegenwert.
4. Wozu braucht man negative Zahlen? Zur Darstellung von Werten unter Null, z.B. Temperaturen.
5. Was ist der Unterschied zwischen -5 und 5? -5 liegt links von Null, 5 rechts davon.
6. Wie multipliziert man negative Zahlen? Minus mal Minus ergibt Plus.
7. Wie dividiert man negative Zahlen? Minus geteilt durch Minus ergibt Plus.
8. Gibt es eine größte negative Zahl? Nein.
Zusammenfassend lässt sich sagen, dass das Rechnen mit negativen Zahlen ein grundlegendes Konzept in der Mathematik ist. Von der Darstellung von Schulden bis zur Beschreibung von Temperaturen unter dem Gefrierpunkt ermöglichen negative Zahlen eine präzise Darstellung von Werten unterhalb des Nullpunkts. Das Verständnis der Addition und Subtraktion negativer Zahlen ist essenziell für viele Bereiche des Lebens, von der Finanzwelt bis zur Physik. Mit den in diesem Artikel vorgestellten Regeln und Beispielen bist du nun bestens gerüstet, um die Welt der negativen Zahlen zu meistern. Beginne noch heute, dein Wissen anzuwenden und entdecke die vielfältigen Möglichkeiten, die dir das Rechnen mit negativen Zahlen bietet.
Kreative geldgeschenke zum 50 geburtstag fur manner
Starker rucken starkes ich ruckenfitness im gym fur millennials
4 bilder 1 wort level 146 die losung und mehr
