Hoe hoog is die balk eigenlijk? Een vraag die zowel in de wiskundeles als in de praktijk vaak opduikt. Of je nu een boekenplank bouwt, een dak ontwerpt of simpelweg de afmetingen van een object wilt weten, het berekenen van de hoogte van een balk is een essentiële vaardigheid.
De hoogte van een balk bepalen kan op verschillende manieren, afhankelijk van de beschikbare informatie. Soms ken je het volume en de basis, andere keren heb je de diagonaal en een zijde. Het is als een puzzel waarbij je de juiste stukjes moet vinden om het complete plaatje te krijgen. In dit artikel duiken we diep in de wereld van balkhoogtes en ontdekken we de verschillende methoden om deze te berekenen.
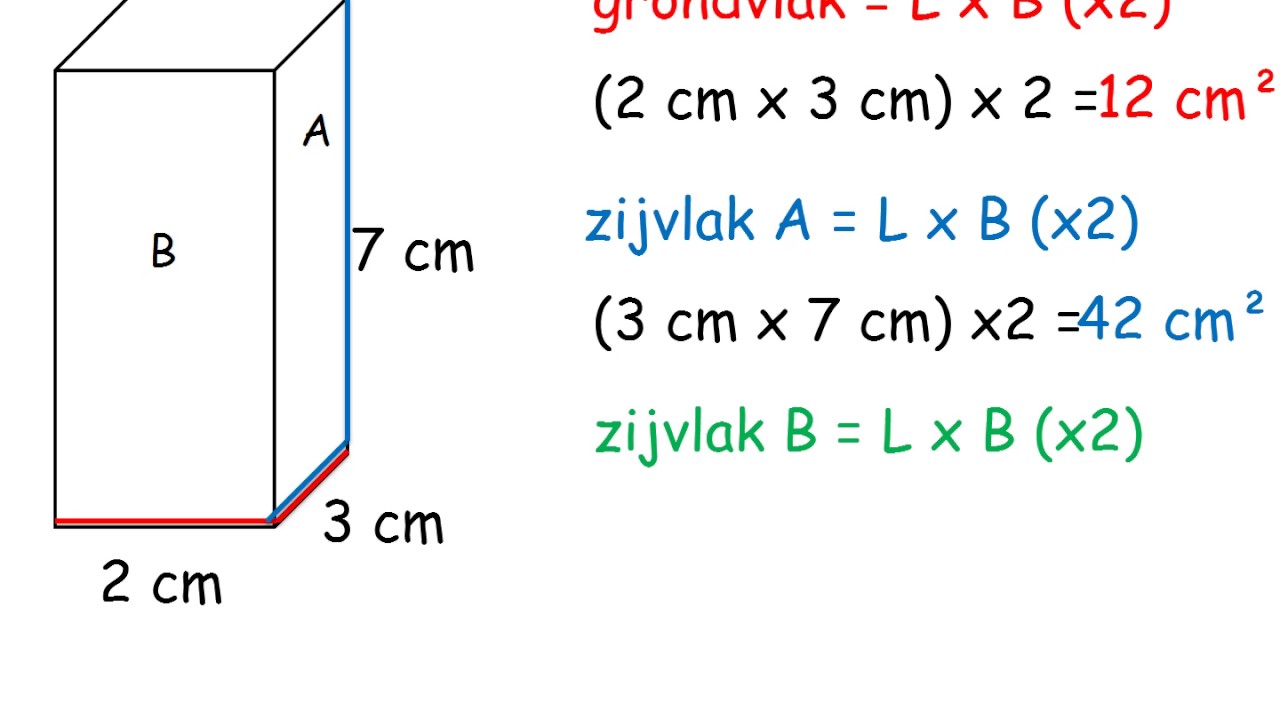
Vanuit een wiskundig perspectief is een balk een driedimensionaal object met een rechthoekige basis. De hoogte is de loodrechte afstand tussen de twee parallelle basisvlakken. Het begrijpen van deze definitie is cruciaal voor het correct toepassen van de formules.
Het berekenen van de hoogte van een balk is al eeuwenlang relevant, van de bouw van de piramides tot moderne architectuur. Het beheersen van deze vaardigheid is niet alleen belangrijk voor professionals, maar ook voor iedereen die met ruimtelijke objecten werkt.
Een veelvoorkomend probleem bij het berekenen van de hoogte is het ontbreken van de juiste gegevens. Het is belangrijk om te identificeren welke informatie beschikbaar is en welke formule daar het beste bij past. Soms is een extra meting nodig om de hoogte te kunnen bepalen.
De formule voor het berekenen van de hoogte is afhankelijk van de beschikbare informatie. Als je het volume (V) en de oppervlakte van de basis (A) kent, is de hoogte (h) gelijk aan V/A. Ken je de diagonaal van een zijvlak (d) en de lengte van de basis (l), dan kun je de hoogte (h) berekenen met de stelling van Pythagoras: h = √(d² - l²).
Voorbeeld 1: Een balk heeft een volume van 120 cm³ en een basisoppervlakte van 20 cm². De hoogte is dan 120 cm³ / 20 cm² = 6 cm. Voorbeeld 2: Een balk heeft een diagonaal van 5 cm en een basislengte van 4 cm. De hoogte is dan √(5² - 4²) = √(25 - 16) = √9 = 3 cm.
Voordelen van het kunnen berekenen van de hoogte van een balk zijn: 1. Nauwkeurige constructie: Het zorgt voor precieze afmetingen bij bouwprojecten. 2. Efficiënt ontwerp: Het helpt bij het optimaliseren van ontwerpen en het minimaliseren van materiaalgebruik. 3. Probleemoplossing: Het stelt je in staat om onbekende afmetingen te bepalen in bestaande structuren.
Checklist: 1. Bepaal welke gegevens je hebt (volume, basisoppervlakte, diagonaal, etc.). 2. Kies de juiste formule op basis van de beschikbare gegevens. 3. Voer de waarden in de formule in en bereken de hoogte.
Stap-voor-stap handleiding: 1. Identificeer de vorm als een balk. 2. Verzamel de nodige gegevens zoals volume, basisoppervlakte, of diagonaal en basislengte. 3. Pas de juiste formule toe. 4. Controleer je antwoord.
Voor- en nadelen van het berekenen van de hoogte van een balk
Er zijn geen directe voor- of nadelen aan het *berekenen* van de hoogte, het is een noodzakelijke handeling. De voor- of nadelen zitten hem in het al dan niet *kennen* van de hoogte.
Beste Praktijken: 1. Maak een schets van de balk met de bekende gegevens. 2. Dubbelcheck je berekeningen. 3. Gebruik de juiste eenheden. 4. Overweeg de nauwkeurigheid van je meetinstrumenten. 5. Vraag feedback van anderen als je twijfelt.
Veelgestelde Vragen: 1. Wat is de formule voor het berekenen van de hoogte van een balk met behulp van volume en basisoppervlakte? A: h = V/A. 2. Hoe bereken je de hoogte als je de diagonaal en basislengte kent? A: h = √(d² - l²). 3. Wat is een balk? A: Een driedimensionaal object met een rechthoekige basis. 4. Waarom is het belangrijk om de hoogte van een balk te kunnen berekenen? A: Voor nauwkeurige constructies en ontwerpen. 5. Welke problemen kunnen zich voordoen bij het berekenen van de hoogte? A: Het ontbreken van de juiste gegevens. 6. Waar kan ik meer informatie vinden over het berekenen van de hoogte van een balk? A: Online wiskunde bronnen en leerboeken. 7. Kan ik een calculator gebruiken om de hoogte te berekenen? A: Ja, een wetenschappelijke calculator is handig. 8. Wat zijn enkele praktische toepassingen van het berekenen van de hoogte van een balk? A: Bouw, architectuur, en ontwerp.
Tips en Trucs: Visualiseer de balk in 3D. Gebruik een meetlint voor nauwkeurige metingen.
Het kunnen berekenen van de hoogte van een balk is een fundamentele vaardigheid die toepassingen heeft in diverse disciplines. Van het bouwen van een huis tot het ontwerpen van een meubelstuk, het begrijpen van de principes en formules is essentieel. Door het beheersen van deze technieken kunnen we nauwkeurige constructies realiseren, efficiënt ontwerpen en problemen oplossen in de driedimensionale wereld. Of je nu een student, professional of hobbyist bent, het investeren in het leren van deze vaardigheid zal je ongetwijfeld ten goede komen. Dus pak je rekenmachine, meetlint en begin met het verkennen van de fascinerende wereld van balkhoogtes! Neem de tijd om te oefenen met verschillende voorbeelden en raadpleeg online bronnen voor extra ondersteuning. Het beheersen van deze vaardigheid zal je zelfvertrouwen vergroten en je in staat stellen om met succes ruimtelijke problemen op te lossen.
Verrukkelijke kippenstoofpot recepten zelfgemaakt
De liefdeswereld van alice munro ontdekken
Verwijder klitten uit kattenvacht de ultieme gids